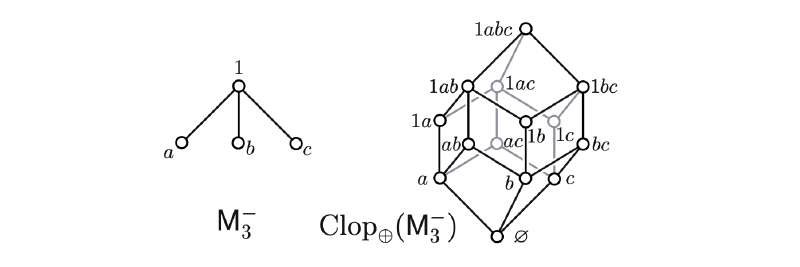
Intro

首先我们提出研究布尔代数的动机，为啥要研究布尔代数？1和0的与、或、非运算是人都能算明白，简直显然到家，为啥还要花篇幅研究这个？首先请考虑以下问题：

• 集合和布尔代数都有De Morgan’s laws，这是巧合吗？

$$ \overline{A \cup B} = \overline{A} \cap \overline{B} \newline \overline{A \cap B} = \overline{A} \cup \overline{B} $$ $$ \overline{A \vee B} = \overline{A} \wedge \overline{B} \newline \overline{A \wedge B} = \overline{A} \vee \overline{B} $$

• XOR和OR哪个运算更fundamental？

• $\vee$和$\wedge$为什么满足双侧分配律？为什么一般的模或向量空间只满足乘法对加法的分配律？分配律的本质是什么？

• 逻辑学与布尔代数有什么关系？逻辑学是研究命题以及命题之间的关系的，布尔代数就是0和1一通操作的代数，这两者有什么关系？

• 为什么电路会跟逻辑相关？电路能实现一切运算吗？

• 很想用抽代的语言来描述布尔代数，具体怎么描述？

希望通过这篇文章，能够解答上述问题。

Boole Algebra $(\mathbb{B^n})$ 和 Boolean Algebra $(K)$ 是不一样的

想到0和1及它们的运算，最先能够联想到的（maybe）是 环 $\mathbb{Z}/2\mathbb{Z}$ 上的运算。我们就从 $\mathbb{Z}/2\mathbb{Z}$ 出发，不断加上结构，首先得到 Boole 代数，然后再得到 Boolean 代数，这也是历史上的发展顺序。

Boole Algebra $(\mathbb{B^n})$

简单起见，我们把 $\mathbb{Z}/2\mathbb{Z}$ 看作特征为2的有限域（而不是环，因为域上向量空间的性质好一点），并将其记作 $\mathbb{B}$:

$$ \mathbb{B} \equiv { \bar{0}, \bar{1} } $$

（下文我们将省略 bar）

很容易验证 $\mathbb{B}$ 上的加法对应 XOR 运算，乘法对应 AND 运算。（从这个角度看，XOR 是比 OR 更fundamental的运算，因为XOR并不依赖任何的电子元件的特征，仅仅是从数学中自然而然引出的概念，即就是 $\mathbb{Z}/2\mathbb{Z}$ 上的加法，仅此而已）。

自然地，我们可以定义 coordinate space $\mathbb{B}^n$，其中的元素是 $n$-tuples of elements of $\mathbb{B}$，并且加法的数乘的定义是 component-wise 的。$\mathbb{B}^n$ 构成 $\mathbb{B}$ 上的向量空间，所以我们称 $\mathbb{B}^n$ 中的元素是一个 bit vector，比如：

$$ \mathbb{B}^5 \ni \mathbf{b} := (1, 0, 1, 1, 0) $$

现在来研究 $\mathbb{B}^n$ 上线性组合、span、dimension 等概念。

Boolean Algebra $(K)$

下面给出 Boolean 代数的定义：

Definition 一个 Boolean 代数 $(K,\vee, \wedge, \bar{} \space)$ 是一个集合 $K$ equipped with 两个二元运算 $\vee$ 和 $\wedge$, 还有一个一元运算 $\space$ $\bar{}$ $\space$, 使得：

A1. $(K, \vee)$ 和 $(K, \wedge)$ 是交换幺半群

A2. $\vee$ 和 $\wedge$ 满足双侧分配律，且二者地位对等

A3. 存在元素 $0, 1 \in K$ 使得:

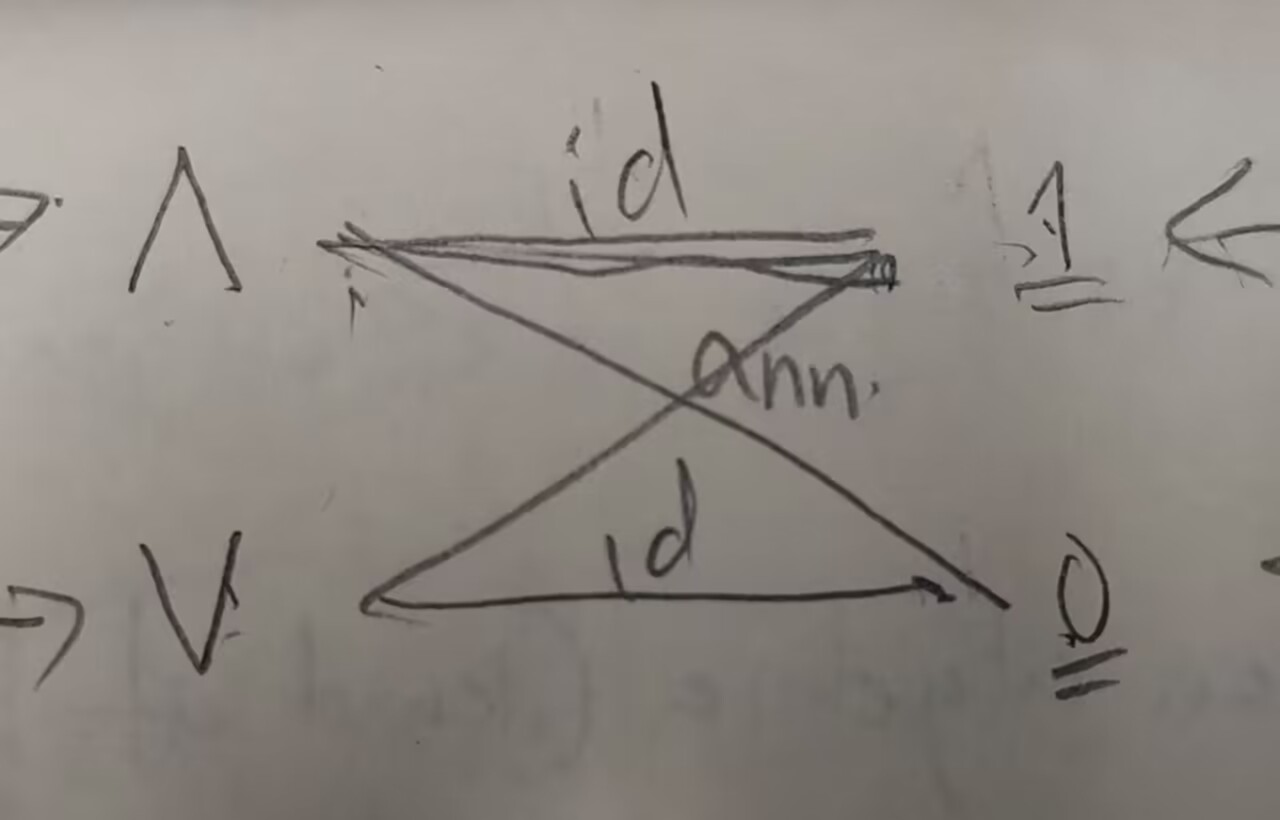
A4. $\space$ $\bar{}$ $\space$ 运算由以下公理定义：

$$ x \wedge \bar{x} = 0 \newline x \vee \bar{x} = 1 $$

A1-A3 称为单调公理，A4 称为补公理。