NOTE:

• 本文仅供个人的学习和参考使用
• 本文参考了UofG尊贵的祖传ppt
• “Others” 中的一般是要通过具体问题来进行学习和理解的部分
• ML 需要大量的实践和数学上的理解，不可能靠本文学懂 ML，这些概念的罗列也只是某种形式教育之下的产物，不必沉迷。

Optimization

基本概念

• 三个要素：decision variables, objective functions and constraints. 任何优化问题先决定这三个分别具体是什么

  • Decision space (决策域) $\mathbb{R}^n$ 和 Feasible Space (可行域) $X$: 有 $n$ 个 decision variables, decision space 的维数就是 $n$; 加上工程学限制，将 decision space 进一步缩小为 feasible space $X$ (比如天线集合参数所有可能的取值集合).

    • Feasible Solution $x$: Feasible Space 中的一个点 $x \in X$, 简称 solution.

  • Objective functions (目标函数):

    • 按 Objective space 分类：
      • 单目标优化： $f(x): X \to \mathbb{R}$
      • 多目标优化 $f(x): X \to \mathbb{R}^m$
    • 按需求分类：
      • Loss function：需要求最小化的一切函数 (最优化方法的默认约定).
      • utility function（效用）：需要求最大值的一切函数.

  • Objective space (目标空间): $f$ 的值所在的空间，$\mathbb{R}$ 或 $\mathbb{R}^n$

• 分类：

  • Constraint / Unconstraint: 无约束是有约束的特例
  • Single-objective / Multi-objective: 看下面
  • Unimodal (Convex) / Multimodal: 有一个最值 / 有多个极值

Single-objective optimization

• 定义：目标函数的值是标量（而不是向量）的问题

  

• Solution的质量：

  • Two feasible solutions: Loss function值越小的solution越好
  • A feasible solution vs. an infeasible solution: 当然feasible solution更好
  • Two infeasible solutions: 哪个超出可行域的程度更低更好

• 分类：

  • Combinational Optimization

    • 定义：决策向量 $x$ 所在的集合是有限阶（离散）的
    • Examples:
      • Traveling Salesman Problem (TSP): 你要从袁记云饺门店出发去五组团、八组团、六组团、格院楼送外卖，最后要回到袁记云饺门店，怎么走最近？
        • 应用：Robot control：应按照哪种顺序使用机械臂才能最大限度地缩短钻孔时间？
      • Quadratic Assignment Problem (QAP): 教学楼有三处地点（有远有近），如何分配地点作为办公室、教室、乒乓球室能使总走路成本最低？（比如老师要经常从办公室到教室，不能太远）。命名为Quadratic的原因是该问题可以用一个二次型来描述。
      • knapsack：你的包只能装20kg的东西，你要旅游只能用包装东西，有手机、拯救者电脑、烧水壶、水杯、卫生纸、杠铃，你带哪些？

  • Continuous Optimization

    • 定义：决策向量 $x$ 所在的集合是连续的
    • Examples:
      • 天线设计：确定天线的长度、宽度、高度等几何参数（在一定范围），使得他的 $S_{11}$ （理解为浪费的能量）Response 在工作波段 5.28 GHz – 5.72 GHz 尽可能小。

Multi-objective optimization

• 定义：多目标优化也叫 Vector Optimization，因为目标函数的取值可看作一个向量

  $$ \min_{x\in X}(f_{1}(x),f_{2}(x),\cdots ,f_{k}(x)) $$

  where $X$ is the feasible space (一般就是 $\mathbb{R}^n$). $x \in X$ is a feasible solution

• 但是往往会有 trade-off 情况：让哪个 $f$ 的值最大呢？但是有一种很显然的情况:

• Solution的质量：

  • $x_1^{*}$ Dominates $x_2^*$: 如果两个 feasible solution $x_1^{*}$ 和 $x_2^{*}$，如果 $x_1^{*}$ 能让所有的 $f$ 都要比用 $x_2^{*}$ 的更小 ( $\le$ )，那 $x_1^{*}$ 肯定优于 $x_2^{*}$，称 $x_1^{*}$ Dominates $x_2^{*}$. 如果是 $<$，称 $x_1^{*}$ strictly dominates $x_2^{*}$.

  • $x_1^{*}$, $x_1^{*}$ Cannot Compare: 如果相较于 $x_1^{*}$，$x_2^{*}$ 会让有些 $f$ 更小有些更大（而不是全部更小或者全部更大），则称 $x_1^{*}$ cannot compared with $x_2^{*}$.

  • $x_1^{*}$ 和 $x_1^{*}$ 要么不能比较，要么一者优于另一者！

• Pareto set 和 Pareto front:

  

  

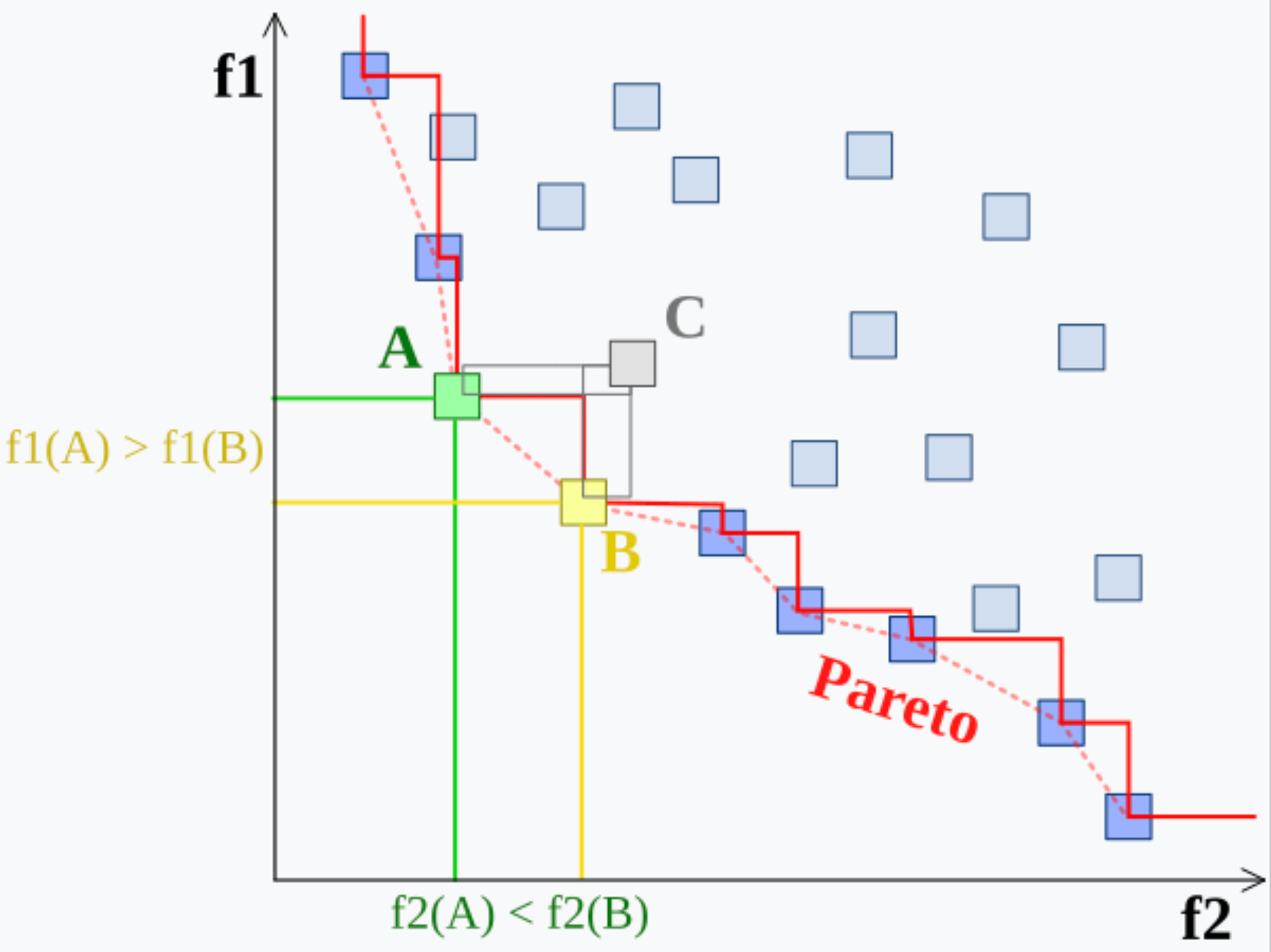
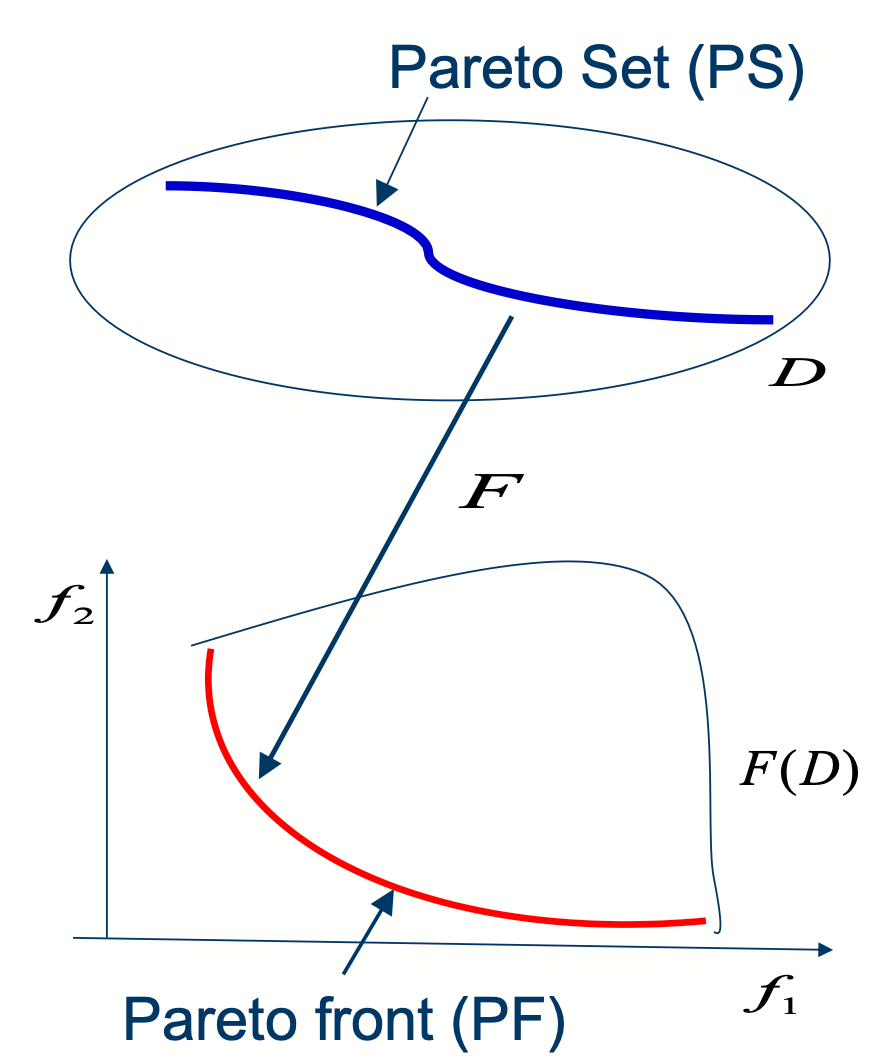
Metric space 度量空间

• Decision space $\mathbb{F}^n$ ($\mathbb{F}$ 是伽罗瓦域) 可被赋予一个特定的 Metric (如欧式距离、Taxi-cab 距离、Hamming 距离) 使之成为一个度量空间

• 其他概念请自行阅读 Rudin 或 Terence Tao 的实分析教材，omitted here.

Others

• 将Engineering问题转化为 Optimization 的问题

AI 部分

Machine Learning (ML) General Concepts

• 一句话概括ML：人先猜一个函数 $f$ 的样子，让机器算出这个函数里面的参数。

• ML 的分类

  

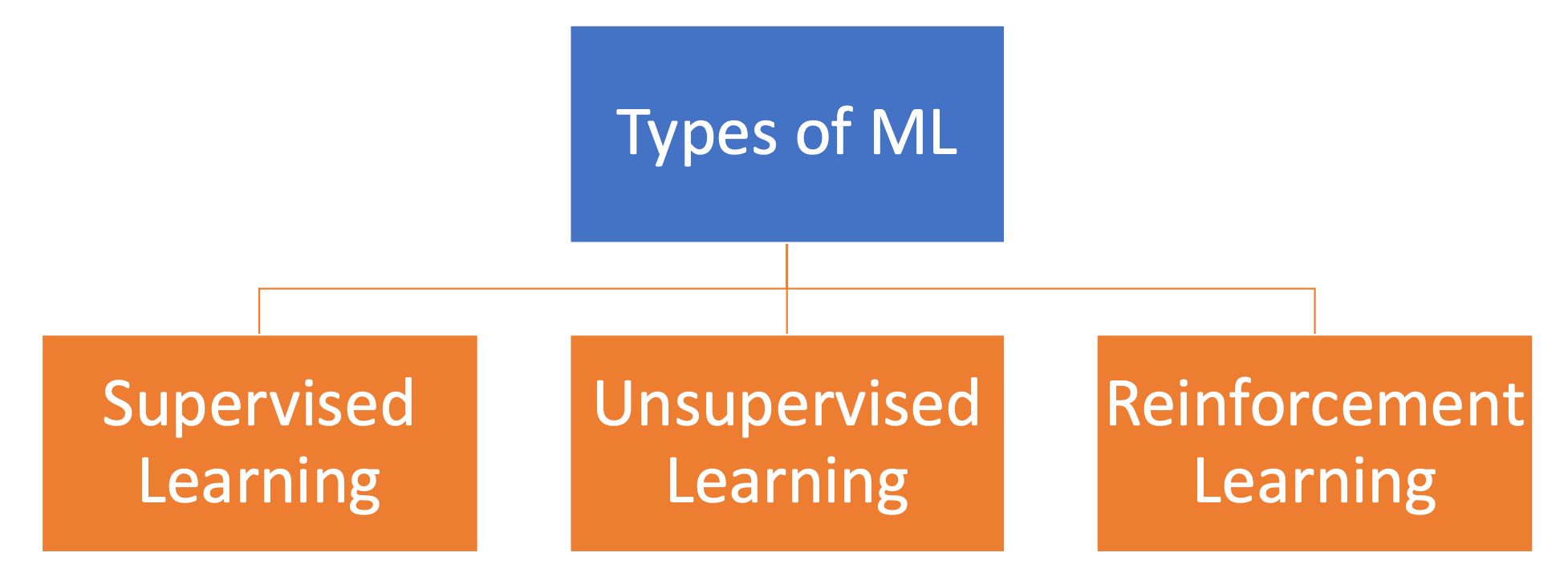
Supervised Learning

Definitions

• Supervised learning: 数据集中有标签的学习.

  • data mining (preparation): 数据集的收集过程
  • data cleaning: 筛选错误的数据的过程
  • Missing data: 对于丢失的数据，丢弃(Dropping)和填补(Imputing)都不太好，因为前者可能使有用的数据损失，后者可能引入偏差 (这ppt写的，无语╰(‵□′)╯)

• (Labelled) Training set $\mathcal{D}$: 一个输入-输出的集合 $\mathcal{D}= {(\mathbf{x_i},y_i)}^N_{i=1}$，$\mathbf{x_i}$ 是输入（比如图片），$y_i$ 是输出（比如类别）

  • Feature Space $\mathcal{X}$: $\mathbf{x_i}$ 的取值集合
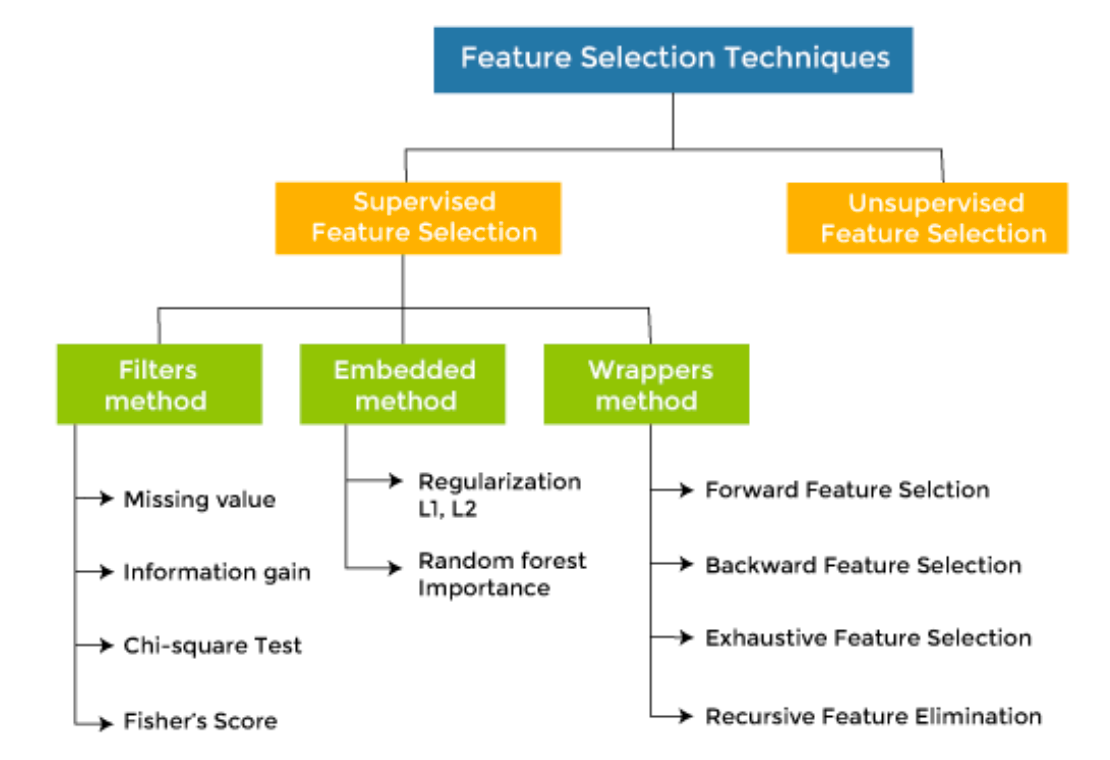
    • Feature Selection: 选择你觉得相关的数据形式（比如生物学研究中，基因表达数据可能包含上万个基因特征，但只有少数基因与某种疾病相关，那就别把这些不相关的数据用来训练了）
  • Label Space $\mathcal{Y}$: $y_i$ 的取值集合

• Supervised learning 解决的问题：

  • Classification 问题（or Pattern recognition: $\mathcal{Y}$ 有限集， $\mathcal{Y} = {1, \ldots, C}$. (比如 {Male, Female})，$y_i$ 称作 categorical variable

    • Binary Classification: $C=2$
    • Multiclass Classification: $C>2$
    • Multilabel Classification: $f$ 为多值映射

    举例：手写数字识别、图片分类

  • regression 问题: $y_i$ 取值于一个无限集 (比如 $\mathbb{R}$)

Unsupervised Learning

Definitions

• Supervised learning: 数据集中没有标签的学习，机器需要自行发现 “interesting patterns” (称为 “knowledge discovery”)。

• (Unlabelled) Training set $\mathcal{D}$: 一个只有输入的集合 $\mathcal{D}= {(\mathbf{x_i})}^N_{i=1}$，$\mathbf{x_i}$ 是输入（比如图片）。

• UnSupervised learning 解决的问题：

  • Clustering: 没有标签的分类问题
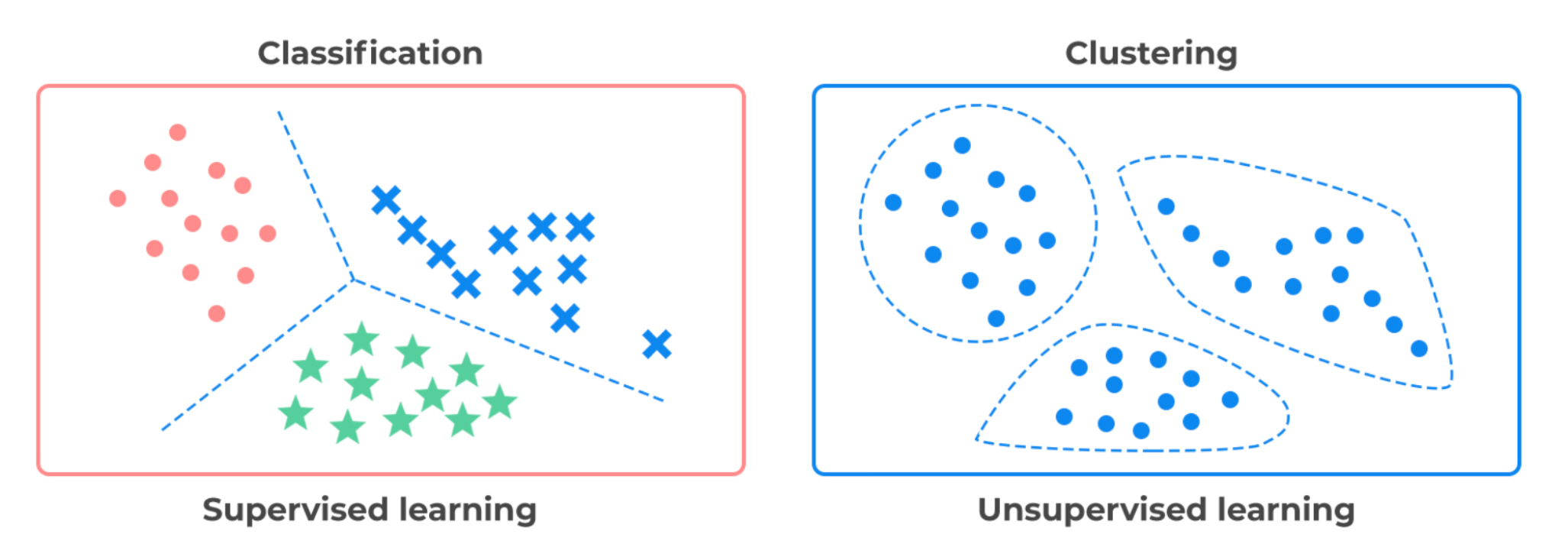
  • Dimensionality reduction: 将数据点降维从而发现影响数据分布的少量几个本质因素(latent factors), 其实很像 Feature Reduction.
    • 常见方法包括：PCA (principal components analysis), ICA (a variation of PCA)

Reinforcement Learning

Definitions

• Reinforcement Learning: 人类也学不会，或者说不清楚怎么学的问题让机器去学的机器学习方法。但是人类知道怎么给奖励或惩罚 (punishment or reward)，使得机器在试错和奖励中学到东西。

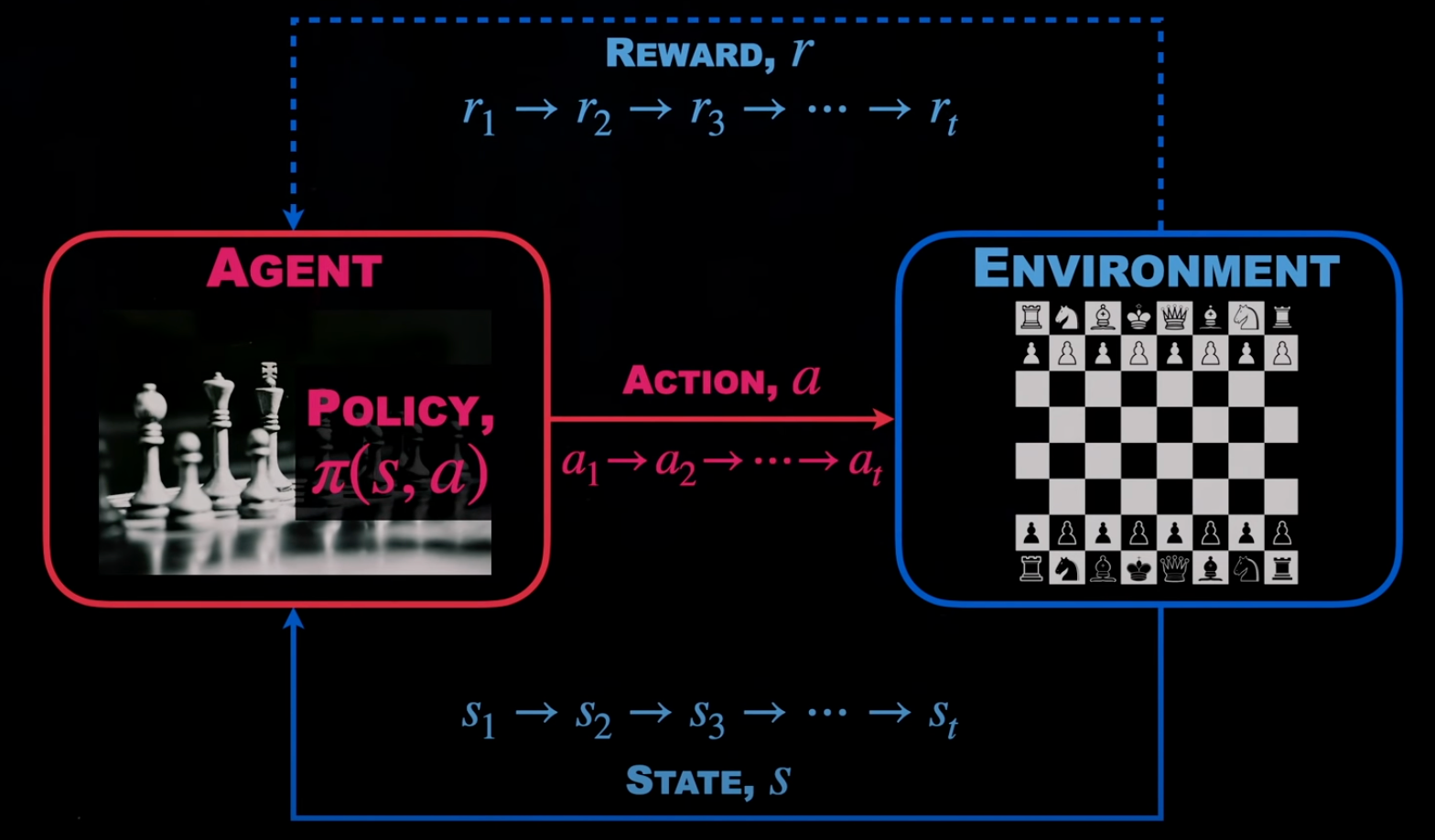
• 方法：（没搞懂）
  • Policy-based RL uses a policy or deterministic strategy that maximises cumulative reward
  • Value-based RL tries to maximise an arbitrary value function
  • Model-based RL creates a virtual model for a certain environment and the agent learns to perform within those constraint