Intro

人类最伟大的成就之一就是发明了集合(set)和映射(mapping)这两个概念。他们的抽象性使得自然界的所有存在都可以被这两个概念描述。比如分类就是图片集合到类别集合的映射，图片生成就是文字集合到图片集合的映射，信源编码就是字符集合到codewords集合的映射，等等。要注意这里的集合都是非常大的！比如图片集合是所有图片，不同大小，黑白的、彩色的等等等等，我们姑且称这种集合为“大集合”吧。比如 $\mathbb{R}$ 到 $\mathbb{R}$ 上所有函数构成的集合(denoted $\mathbb{R}^{\mathbb{R}}$)，这也是“大集合”，这种集合在实践中很难把握和分析。

说回映射，他们往往都是在人脑中发生的，比如我们看到一张图片，立即认为这是这是一条狗而不是其他的东西，即把图片映成拉狗这个对象，但这个映射写不出表达式！

或者说，可以？！如果我们粗略地写出了某种表达式，且图片通过这个表达式输出的结果和人脑中输出的结果很像，那是不是可以说我们找到了这种映射的显式表达？

这正是机器学习干的事情，我们尝试找到一种映射，定义域是所有图片的集合(for example)，值域是物品字符串的集合。如果我们把所有图片到物品字符串的映射也都收集在一起构成一个“大集合”（或称为大函数空间），其实我们要找的就是这个大函数空间中的一个元素！注意是元素，这个元素就是我们脑中的那个映射。

但是怎么找呢？首先这个映射都没有一个固定的形式，比如它可以是 $y=ax^2$，也可以是 $y = \sin(ax)+bx+cx^2+d\log(x)$ 等等所有这样的表达式 (这里简单起见就用一维变量的来说明)。如果我们仅仅把问题就局限在某种特定的函数形式上，这个过程就叫参数化(parametrization)，这里的 $a, b, c, d$ 就叫做参数(parameters)。某一种特定的参数化，远远不能涵盖大函数空间中的所有元素！

但是有一种参数化形式，它几乎能涵盖整个函数空间！！也就是说，我们只需要考虑这一种形式的函数，就几乎相当于考虑了函数空间的所有函数！这怎么可能呢？当然上面举例的两种参数化显然是不行的，你能想出什么样的映射形式能够“逼近”大函数空间中的任何映射？

Universal approximation theorem

这种参数化长这样：

$$ y = \sum_{i=1}^m c_i , \sigma(w_i \cdot x + b_i)
$$

其中 $\sigma(.)$ 是一种给定的具体的非线性函数，$w_i$, $b_i$, $c_i$都是参数。$x$ 是哪个集合里面的？我知道你很急，但你先别急，总之你看到了一种特殊的参数化形式，现在我跟你说它能拟合任意的函数！

如果只有三个参数的话，提供的自由度只有三个，肯定不行。所以它们其实是很多很多（但有限个）参数，只是分成了三类。如果能将这种参数话形式可视化出来就好了，有什么方法呢？

这种形式的函数都可以表示成这个样子：

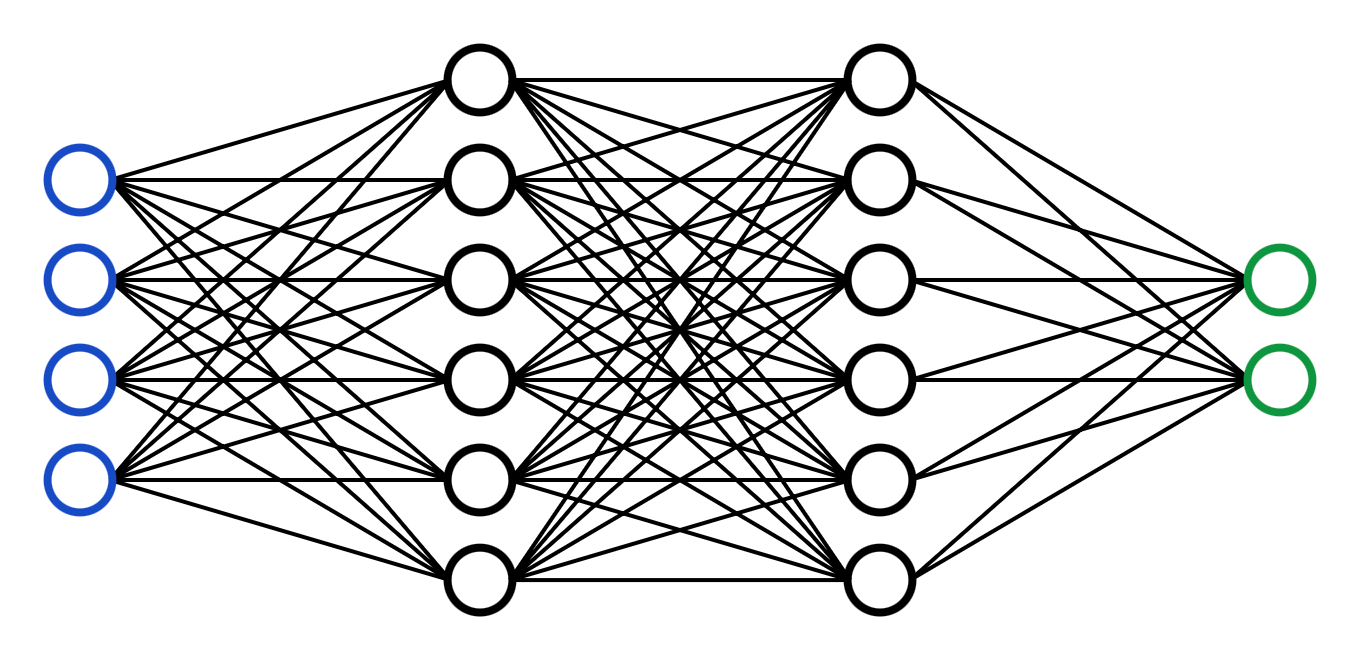
称为（全连接的）“神经网络”。

神经网络可以拟合任意函数。

这个结论使得机器学习得以安稳地存在，因为我们知道理论上，只要网络足够复杂，就可以拟合出任意的映射（而不会忙活半天最终证明压根拟合不了！）