Draft

Data Structure and Algorithm Notes 数据结构与算法笔记

CN-blogs
Updating
Author

Marcobisky

Published

October 21, 2025

本章语言以 Python 为主, 面试时需要背下文中的函数而不能靠 vibe coding.

本章 abbr: ITV: Interview 回答方法

1 Time/Space Complexity 时间/空间复杂度

  • 时间看循环, 空间看数组

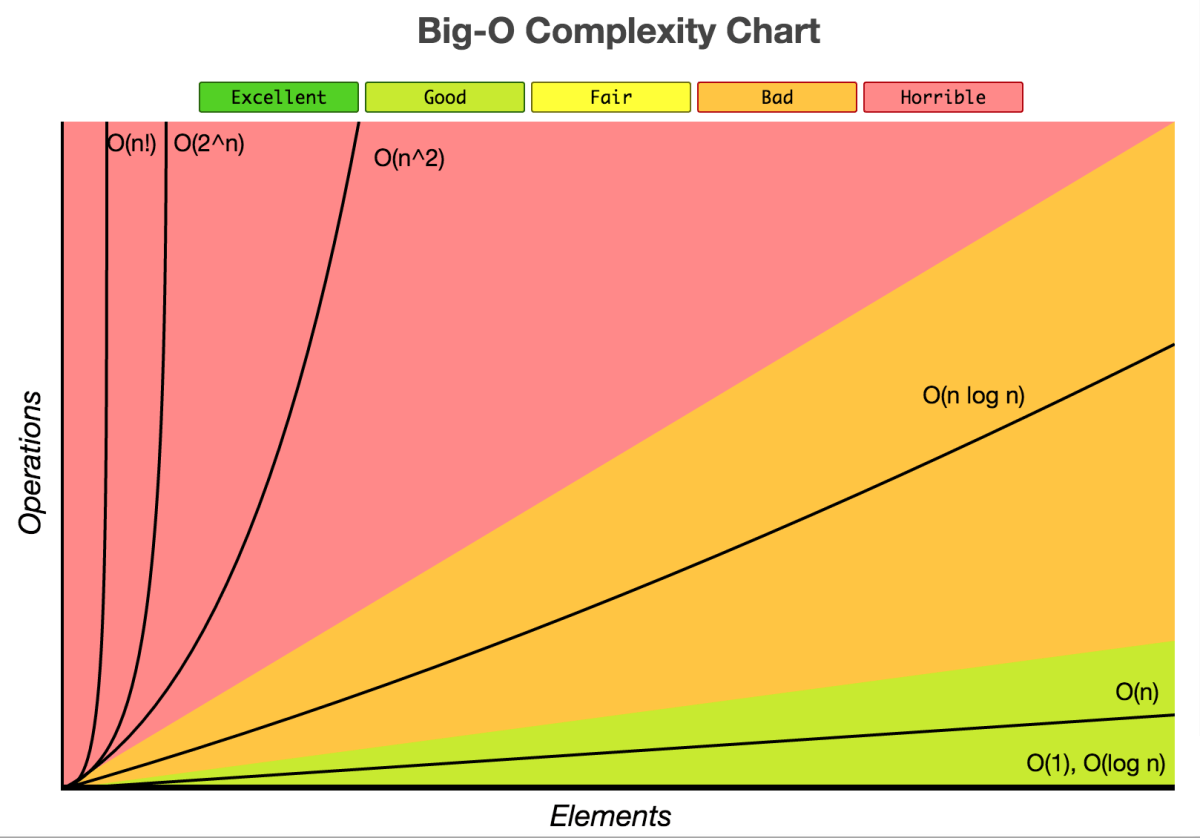
    Time Complexity 不 care 系数, 只 care 随着问题 elements 规模的增长 operations 数量的增长情况

    \(\mathcal{O}(n \log n)\) 这种想象成循环嵌套, \(\mathcal{O}(n+m)\) 这种想象成循环并列

  • 大部分算法停机时间不确定, 用最坏情况来思考复杂度!

  • 空间复杂度一般都是 \(\mathcal{O}(1)\) 或 \(\mathcal{O}(n)\), \(\mathcal{O}(n^2)\) 比较少, \(\mathcal{O}(n)\) 和 \(\mathcal{O}(n\log n)\) 非常少.

    • 递归一般会有个 \(\mathcal{O}(n)\), 因为要用到递归栈.

  • 时间和空间是 trade-off 关系, 二者只能求其一. 一般来说, 由于空间 cheap, 时间贵, 所以更看重时间复杂度.

2 Data Structure 数据结构

2.1 General 共性

  • 所有数据结构都要考虑1以下做操作 (abbr. ASID) 是否方便 (时间复杂度):
    • Access 访问: index 找 element (数组)
    • Search 搜索: element 找 index (数组)
    • Insertion 插入
    • Deletion 删除

1 ITV 请对比两个数据结构.

2.2 Array 数组

  • Array 数组: 连续内存空间! 相同类型数据!
Figure 1: 区分元素和索引

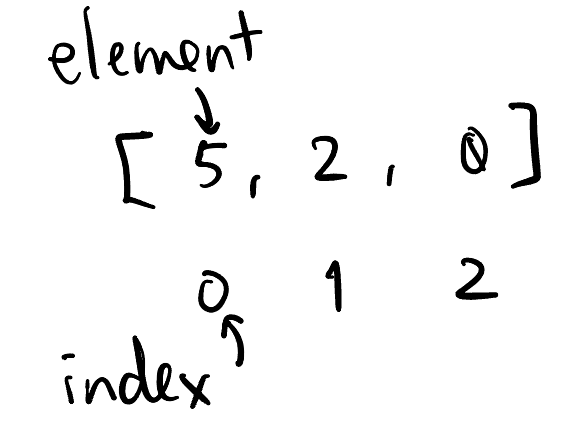
  • 区分: Element 元素 vs Index 索引 (Figure 1)

  • ASID: \(\mathcal{O}(1)\), \(\mathcal{O}(n)\), \(\mathcal{O}(n)\), \(\mathcal{O}(n)\)

    • 适合读多写少的场景.
    • 但是 append 操作是 \(\mathcal{O}(1)\) 的.
Python 具体操作方法

Check list: