Probability Theory Takeaways 概率论极简笔记

Analysis
CN-blogs
一套测度论语言的概率论极简笔记
Author

Marcobisky

Published

November 5, 2025

1 Spaces 空间

  • Sample Space 样本空间 \(\Omega\): 任何 Set 集合

    • Example: 抛一个骰子的样本空间 \(\Omega = \{\text{``1''}, \text{``2''}, \text{``3''}, \text{``4''}, \text{``5''}, \text{``6''}\}\), 注意集合里面的元素是字符串 (或者其它能代表能抛出的点数的象征符号, 一句话, 一张图片, 一个表情 / 心情都可以), 最好不要理解为数字!
    • Outcome 实验结果: 样本空间中的元素. 理解为 “The result of a single trial of the experiment.”

  • Event Space 事件空间 \(\mathcal{A}\): Measurable Space 可测空间

    • Example: 抛一个骰子的事件空间 \(\mathcal{A} = \{\text{``1''}, \text{``2''}, \text{``3''}, \text{``4''}, \text{``5''}, \text{``6''}, \text{``1 or 2''}, \text{``1 or 3''}, \cdots, \Omega, \varnothing\}\)
    • Event 事件: 可测集, Event Space 中的元素. 理解为 “A meaningful statement about the experiment.”
    • Event occurs 事件发生: 某个 outcome 属于某个 event: \[A \in \mathcal{A} \text{ occurs } :\iff \text{outcome } s \in A.\]

  • Probability Space 概率空间 \((\Omega, \mathcal{A}, \mathbb{P})\): Measure Space 测度空间

    • Conditional Probability 条件概率: 事件 \(B\) 诱导的概率测度 (\(\mathbb{P}_B(A)\) 常记作 \(\mathbb{P}(A|B)\)): \[ \mathbb{P}_B (A) := \begin{cases} \frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)}, & \mathbb{P}(B) > 0 \\ 0, & \mathbb{P}(B) = 0 \end{cases} \]

2 Random Variable 随机变量

  • RV (Random Variable) 随机变量 \(X\): Measurable Mapping 可测映射 (注意并不需要定义概率测度!)

    • Motivation: 将陌生的 event space 映射到熟悉的 \(\mathbb{R}\) (或 \(\mathbb{R}^n\) 等), 这个映射是可测空间的同态, 信息量只有可能减少不会增加, 这个信息量的减少说明我们希望通过 RV 来量化 event space 中我们关心的部分, 丢弃不关心的部分, 理解为 “A measurement of interest in the context of the experiment”, 比如:

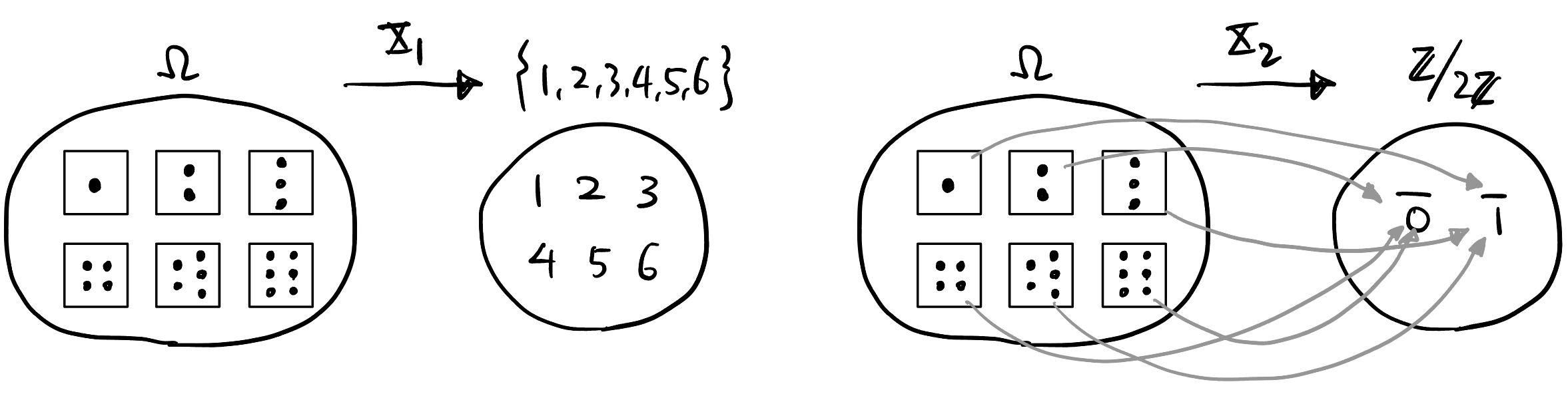
      Figure 1: 定义 \(X_1\) 说明我们关心问题的全貌 (\(X_1\) 没有损失信息量, 忠实 (faithful) 地表现了抛骰子出现的各种情况); 定义 \(X_2\) 说明我们只关心抛骰子的点数是奇数还是偶数.

    • Abuse of notation: \(X^{-1}(A)\) 常记作 \(\{\omega \in \Omega | X(\omega) \in A\}\), 比如 \(X^{-1}([a, b]) \equiv \{\omega \in \Omega | X(\omega) \in [a, b]\}\).

  • RV 的分类

    • Discrete RV 离散随机变量: Codomain 是 countable set (\(\aleph_0\)) 可数集的 RV.
    • Random number 随机数: Codomain 是 \(\mathbb{R}\) 的 RV.
    • Random vector 随机向量: Codomain 是 \(\mathbb{R}^n\) 的 RV.
    • Random matrix 随机矩阵: Codomain 是 \(\mathbb{R}^{m \times n}\) 的 RV.
事件的独立和随机变量的独立
  • 事件的独立: 事件 \(A,B \in \mathcal{A}\) 独立指 \(\mathbb{P}_A = \mathbb{P}_B = \mathbb{P}\), 即 A (或 B) 诱导出来的测度不变.
    • 事件 \(A, B\) 独立也称他们 不相关 (uncorrelated).
  • 随机变量的独立: RV \(X, Y\) 独立指对任意 \(S, T\) (分别是 \(X, Y\) 的 codomain 上的可测集), 事件 \(X^{-1}(S)\) 和 \(Y^{-1}(T)\) 独立.
    • 注意我们用任意原像事件的独立性来定义 RV 独立性.
    • 可以推出 RV 独立性等价于: Joint CDF/PDF 等于各自 CDF/PDF 的乘积 (证明略).
    • 进而可以推出 (不等价!) \[\mathbb{E}[XY] = \mathbb{E}[X] \mathbb{E}[Y].\]

2.1 Algebra of RV 代数结构

  • Codomain 为 \(\mathbb{R}^n\) 的 RV 构成交换代数 (继承了 \(\mathbb{R}^n\)).
    • Distribution 分布: \(\mathbb{R}\) 推前到 \((\mathbb{R}^n, \mathcal{B}(\mathbb{R}^n))\) 的 Pushforward Measure \(X_* \mathbb{P}\) (一般记作 \(\mathbb{P}_X\), though).
      • Joint Distribution 联合分布: 对于多个相同样本空间1!上的 RV 可以定义他们的联合分布. 严谨数学语言较为麻烦 (omitted).
      • Marginal Distribution 边缘分布: 联合分布的某些变量的投影 (omitted).
    • CDF 累积分布函数 \(F_X\): Codomain 有序结构即可定义 CDF: \[F_X(x) := \mathbb{P}_X ((-\infty, x]).\]
    • PDF 概率密度函数 \(f_X\): CDF 的 Radon-Nikodym 导数, 满足: \[\mathbb{P}_X(B) = \int_B f_X \mathrm{d} \lambda, \forall B \in \mathcal{B}(\mathbb{R}).\] (\(\lambda\) 是 \(\mathbb{R}\) 上的 Lebesgue 测度)
      • PMF 概率质量函数: 离散 RV 的 PDF. \[\mathbb{P}_X(A) = \int_A f_X \mathrm{d} \# = \sum_{x \in A} f_X(x), \forall A \in \mathcal{P}(X).\] (\(\#\) 是离散测度空间的 counting measure)

1 Joint RV / distribution: 同一个样本空间, 不同 codomain, Product measure space: 很多个不同的样本空间, 通过 product 操作构造出一个大的空间.

  • Expectation 期望: 就是积分 \[ \mathbb{E}[X] := \int_{\Omega} X \mathrm{d} \mathbb{P}. \]

    • 由积分的性质显然有: \[\mathbb{E}[aX + bY] = a \mathbb{E}[X] + b \mathbb{E}[Y].\]

  • Inner Product 内积: (由 Algebra 知 \(XY\) 也是 RV.) \[ \langle X, Y \rangle := \mathbb{E}[XY]. \]

    • Covariance 协方差: centered 后的内积, let \(X_c \equiv X - \mathbb{E}[X]\), \[\operatorname{cov}(X, Y) := \langle X_c, Y_c \rangle.\]
      • Variance 方差: 自协方差 / center \(X\) 2-norm 的平方. \[\operatorname{var}(X) := \operatorname{cov}(X, X) = \|X_c\|_2^2.\]
      • 2nd Moment 二阶矩: 不 center 的 \(X\) 2-norm 的平方. \[\mathbb{E}[X^2] = \|X\|_2^2.\]
    • Correlation 相关系数: 归一化后的协方差. \[\operatorname{cor}(X, Y) := \frac{\operatorname{cov}(X, Y)}{\sqrt{\operatorname{var}(X) \operatorname{var}(Y)}}.\]

  • Metric 度量 (注意 \(t\) 是 \(\Omega\) 映到单点集 \(\{t\}\) 的 RV 而不是实数):

    • RMSE (Root Mean Square Error) 均方根度量: \[d_2(X, t) := \|X - t\|_2 = \sqrt{\mathbb{E}[(X - t)^2]}.\]
    • MAE (Mean Absolute Error) 平均绝对误差度量: \[d_1(X, t) := \|X - t\|_1 = \mathbb{E}[|X - t|].\]

2.2 Series of RV 随机变量序列

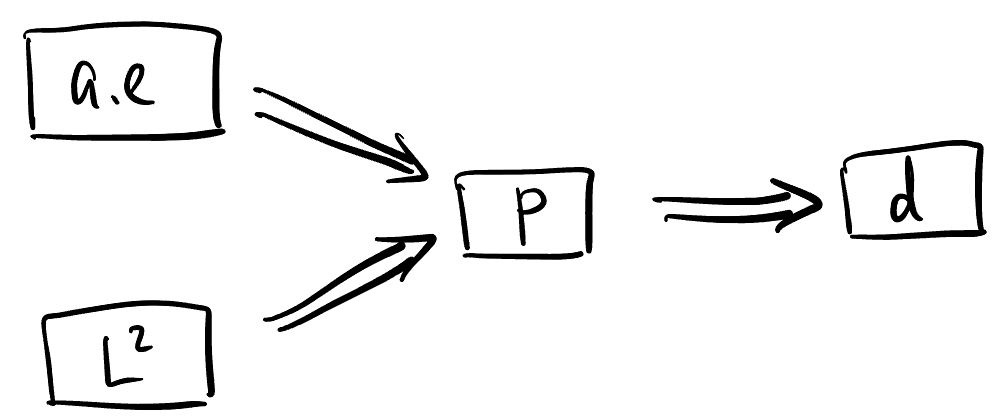
  • Convergence 收敛方式: \((X_n)\) 可以以下几种方式收敛到 \(X\):
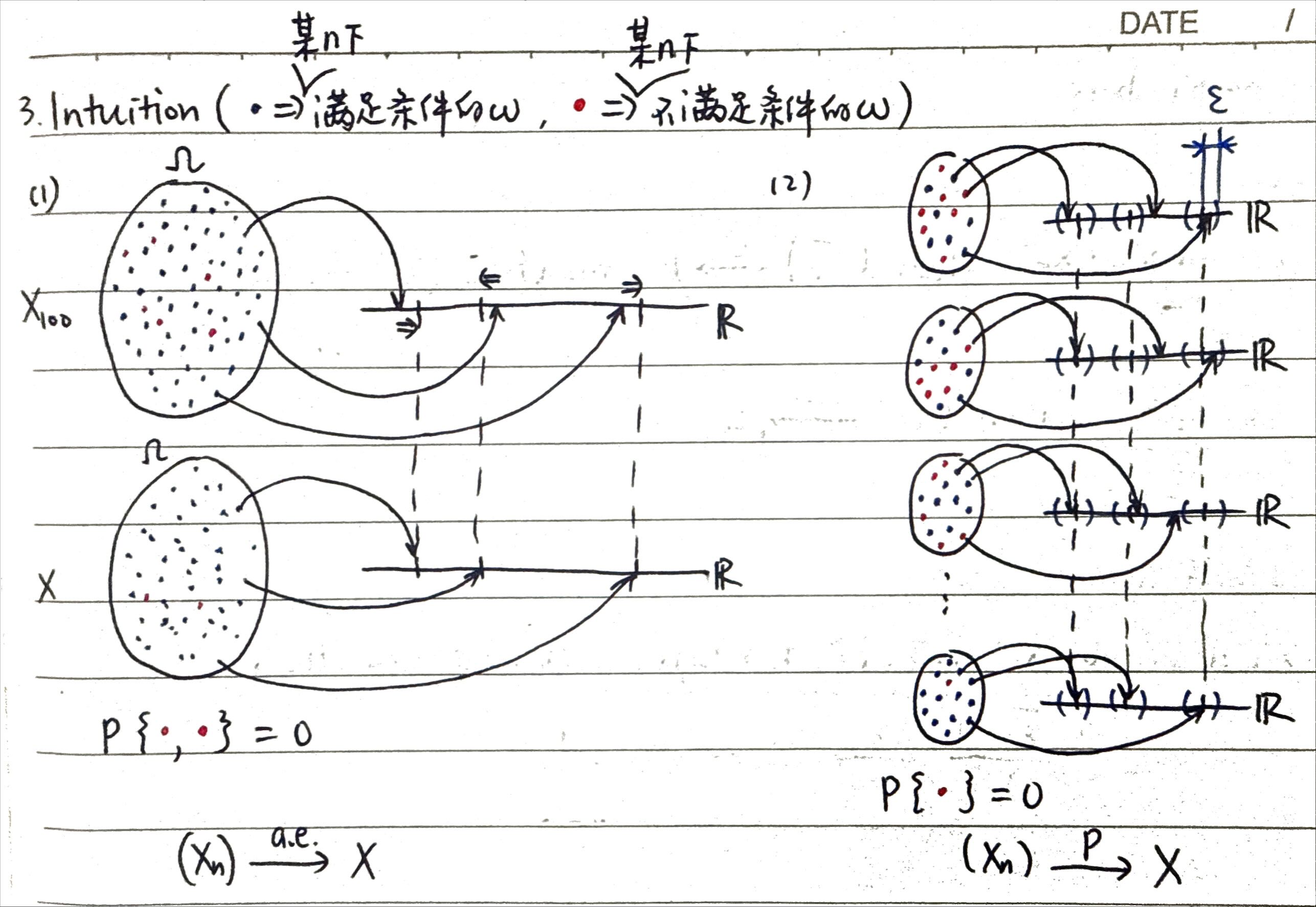
    • Almost everywhere (a.e.) 几乎处处收敛: 即 \((X_n)\) 几乎处处逐点收敛到 \(X\), i.e., \[\mathbb{P}(\{\omega \in \Omega : \lim_{n \to \infty} X_n(\omega) = X(\omega)\}) = 1.\]
    • In probability 依概率收敛: 不一致收敛的点的测度趋于 0, i.e., \[\mathbb{P}(\{\omega \in \Omega : |X_n(\omega) - X(\omega)| \ge \varepsilon\}) \to 0, \forall \varepsilon > 0\]
    • In distribution 依分布收敛: \(F_{X_n}\) (在所有 \(X\) 的 CDF 的连续点上) 逐点收敛到 \(F_X\), i.e., \[F_{X_n}(x) \to F_X(x), \forall x \text{ is a continuity point of } F_X.\]
    • \(L^p\) 收敛: \(X_n\) 与 \(X\) 的 \(L^p\) 距离趋于 0, i.e., \[\|X_n - X\|_p \to 0.\]
收敛方式的关系
Figure 2: 四种收敛的关系
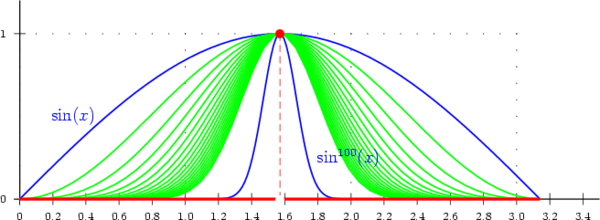
  • 函数的 pointwise 收敛比 uniform 收敛弱 (Figure 3), 但是可测函数的 a.e. 收敛比 依概率收敛强!
Figure 4: (1) 几乎每个点最终都进入了 \(\varepsilon\) 邻域; (2) 进入 \(varepsilon\) 的蓝色点集会变化! (当然满足 uniformly cvg 的点集也会变化) 但如果在概率的条件下考虑这个问题, 进入的点集变化地更为疯狂, 以至于可能表面看上去所有的点都进去了, 其实单看每个点只是在极限附近徘徊不定 (不一定是几乎处处的点的)
Figure 5: 一个经典的依概率收敛而不几乎处处收敛的「扫区间」序列
Figure 3: 逐点收敛的函数列极限可以不连续

2.3 Law of Large Numbers 大数定律

(强) 大数定律

Theorem 1 \(X_n\) i.i.d. with mean \(\mu\), then \[(\overline{X_n}) \xrightarrow{a.e.} \mu.\]

  • 弱大数定律: 根据 Figure 2 改成依概率收敛 (有何意义?)

  • 注意 \((\overline{X_n})\) 也是 RV 序列; \(\mu\) 是单点 RV (而不是单纯的实数)! 不要将 RV 的代数运算结果看成数字!!

  • 意义: 使得我们可以以任意小的误差测量一个随机实验的均值! 这个定理过于「显然」以至于我们在不经意间就用到了它, 比如测量抛硬币的均值 (0.5) 时, 我们会很自然地抛很多次硬币获得「结果」然后取均值, 这样测出来的值并不是「抛一次硬币的随机变量」的均值, 而是「抛 \(n\) 次硬币, 每次的点数相加后除以抛的次数, 这个随机变量坍缩后的值」, 这是完全两个随机变量! 后者坍缩后的值几乎不变, 于是我们将它看作后者随机变量 (并非前者) 的均值. 而正因为有大数定律, 这个值才可以与前者的均值以任意误差接近.

    • In other words, 当一件「随机」的实验被概率建模时, 平行宇宙视角的「均值」(只进行一次实验, 但是在上帝视角收集不同平行宇宙的结果, “ensemble average”) 等于时间平均视角 (让时间流逝, 建立新的样本空间 \(\Omega^{\otimes n}\), “time average”) 后的「均值」.

  • 允许用 time average 来估计 ensemble average 的随机过程被称为 ergodic process 遍历过程, 大数定律是遍历过程的特例.

2.4 Central Limit Theorem 中心极限定理

  • 中心极限定理还告诉了我们 \(\overline{X_n}\) 的形状 (分布): 竟然跟 \(X_i\) 的分布无关, 都近似于 Gaussian 分布!
中心极限定理

Theorem 2 (Without loss of generality) (X_n) i.i.d. with mean \(0\) and variance \(\sigma^2\), then \[\overline{X_n} \xrightarrow{d} \mathcal{N}\left(0, \frac{\sigma^2}{n}\right).\]

3 Distribution 常见分布

  • Bernoulli: \(X \sim \operatorname{Ber}(p)\) 不均匀的硬币.

  • Binomial: \(X \sim B(n, p)\) 固定次数 \(n\) 数正面. E.g., 好评数量.

  • Negative Binomial: \(X \sim NB(s, p)\) 跟 Binomial 操作相反, 固定正面数 (s, success) 总次数.

    • Geometric: \(X \sim G(p)\) 特例, \(s=1\).

  • Hypergeometric: \(X \sim H(n, s, f)\), 不放回版本的 Binomial (initial \(p = s / (s+f)\))

  • Poisson: \(X \sim \operatorname{Pois}(\lambda)\), 连续版本的 Binomial (离散化后 \(\lambda\) 退化为 \(p / n\)). E.g., 单位时间顾客到达数.

    • Exponential: \(X \sim \operatorname{Exp}(\lambda)\), 跟 Poisson 操作相反. E.g., 顾客到达的时间间隔.